조컴공은 오전의 수업을 다 듣고나서 IT융합대학 건물에서 나오고 있다.

이제 다음 수업까지 \(K\)분의 공강시간이 남아있다. 이 시간 동안에 컴공이는 캠퍼스를 산책하려 한다.

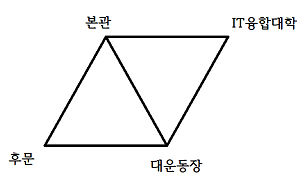
컴공이는 본관, IT융합대학, 후문, 대운동장을 산책하는 것이 명상에 가장 도움이 된다고 생각했다.

산책 중에는 이 네 곳을 자유롭게 이동할 수 있지만, 위 그림에 나타난 것처럼 IT융합대학과 후문 사이는 직접 이동이 불가능하다.

한 장소에서 다른 장소로 이동할 때는 항상 \(10\)분이 소요되며, 이동 도중에 경로를 이탈하거나 뒤돌아서거나 멈춰서지 않는다.

그리고 \(K\)분 후에 정확히 IT융합대학에 도착하면 그것은 올바른 산책의 경로가 된다.

컴공이는 매번 산책이 되는 경로를 다르게 하고 싶다.

즉, 이전에 산책해봤던 경로와 이번에 산책할 경로가 완전히 일치해서는 안 된다.

경로가 되는 경우의 수는 무한하지 않기 때문에, 언젠가 경로가 바닥나면 산책을 중단해야 할 것이다.

그렇다면, 컴공이는 총 몇 번을 산책할 수 있을까?

가령, \(K = 20\)인 경우를 생각해 보자.

이때는 총 \(2\)번 이동이 가능하다. 가능한 모든 경우는

• IT융합대학 → 본관 → IT융합대학
• IT융합대학 → 본관 → 후문
• IT융합대학 → 본관 → 대운동장
• IT융합대학 → 대운동장 → IT융합대학
• IT융합대학 → 대운동장 → 후문
• IT융합대학 → 대운동장 → 본관

이고, 마지막에 IT융합대학에 도착하는 경우는 \(2\)가지가 있다. 즉 \(2\)번 산책이 가능하다.

입력

• 첫 번째 줄에 \(K\)가 주어진다. \((0 ≤ K ≤ 1,000,000)\), \(K\)는 \(10\)의 배수

출력

• 경로가 될 수 있는 모든 경우의 수를 \(10007\)로 나눈 나머지를 출력한다.

입력 예시 1

20

출력 예시 1

2

입력 예시 2

70

출력 예시 2

130

힌트

• 수가 빠르게 커지기 때문에 계산 과정에서 10007로 MOD하지 않으면 오버플로우가 발생한다.
• (A + B + C + D + ...) % MOD = (((A + B) % MOD + C) % MOD + D) % MOD + ... 이고, 계산 도중에 발생하는 오버플로우를 막기 위해 우변에 있는 수식처럼 사용해야 한다.