4. 인싸 컴공이(하)
View as PDF조컴공은 평행세계에 존재하는 다른 조선대학교에 다니고 있다.
그곳의 조선대학교에도 IT융합대학이 있는데,
대학 건물은 \(N\)층으로 이루어져 있고 북측 계단, 중앙 계단, 남측 계단을 통해 1층 단위로 오르내릴 수 있다.
현재 엘리베이터가 고장나 있어서 엘리베이터를 이용할 수 없다.
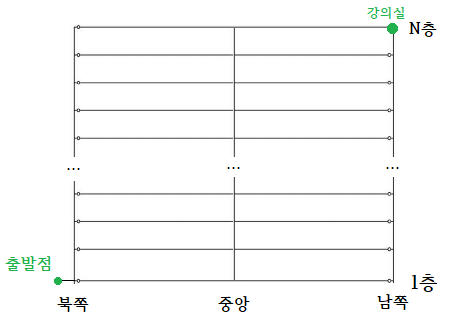
컴공이는 1층 북쪽 끝에 있는 문으로 들어와서 \(N\)층 남쪽 끝에 있는 강의실로 가려고 한다.
지각하면 안 되기 때문에 남쪽 또는 윗층으로만 이동할 수 있고, 북쪽이나 아랫층으로는 갈 수 없다.
컴공이는 학생들과 교수들도 인정하는 인싸이며, 강의실까지 가는 도중에 최대한 많은 친구들을 만나려고 한다.
친구들은 항상 경로의 정점(꼭짓점)에 서 있고 각 정점에 있는 친구의 수를 미리 알고 있을 때
컴공이가 만날 수 있는 가장 많은 친구의 수를 알아내보자.
입력
- 첫 번째 줄에는 \(N\)이 주어진다.\((1≤N≤1,000)\)
- 다음 \(N\)줄에 걸쳐 1층부터 \(N\)층까지 북쪽, 중앙, 남쪽 정점에 있는 친구의 수가 한 칸으로 구분되어 주어진다.(각 친구의 수는 \(1,000\) 이하의 음이 아닌 정수이다.)
출력
- 컴공이가 만날 수 있는 가장 많은 친구의 수를 출력한다.
입력 예시 1
3
1 0 0
1 0 1
0 0 1
출력 예시 1
4
Comments
이 문제도 우리 교재에서 소개되었던 문제의 변형입니다. 어떤 문제일까요? 바로 행렬의 최대값 경로 문제입니다. 위의 그림을 어떻게 행렬로 표현할지.. 표현이 되면, 이 문제에서는 유효한 이동은 우향 이동과 상향이동만 있지요? 그럼 문제의 답을 도출할 수 있는 재귀 구조를 정의할 수 있습니다.